Arrays are a collection of variables of the same data type. They are useful for storing and organizing data and can be sorted when the data needs to be in a specific order. For example, if you have a list of names you want to display alphabetically, you need to sort the array of names first.
Whether you want to sort an array of integers in ascending order or an array of objects using a custom comparator, Java has you covered. In this article, we will explore the various ways to sort an array in Java, including using the built-in Arrays.sort() method, a Comparator, and custom sorting algorithms, like selection sort, insertion sort, and bubble sort.
Sorting an Array with Arrays.sort() in Java
Sorting an array in Java is a common task that can be accomplished with the Arrays.sort() method. This built-in function allows you to quickly and easily sort an array of integers or objects.
To use Arrays.sort(), simply pass in the array that you want to sort as an argument. For example, to sort an array of integers in ascending order, you can use the following code:
int[] numbers = {5, 2, 7, 1, 3};
Arrays.sort(numbers);
The resulting sorted array will be [1, 2, 3, 5, 7].
After this line of code is executed, the numbers array will be sorted and will contain the values 1, 2, 3, 5, 7.
Let’s take another example. Let’s say you have an array of Person objects that you want to sort by their last name:
Person[] people = {new Person("John", "Doe"), new Person("Jane", "Doe"), new Person("Bob", "Smith")};
Arrays.sort(people);
For this to work, the Person class must implement the Comparable interface and override the compareTo() method to specify the ordering criteria. For example:
public class Person implements Comparable<Person> {
private String firstName;
private String lastName;
public Person(String firstName, String lastName) {
this.firstName = firstName;
this.lastName = lastName;
}
public String getFirstName() {
return firstName;
}
public String getLastName() {
return lastName;
}
@Override
public int compareTo(Person other) {
return this.lastName.compareTo(other.getLastName());
}
}
Now, when you call Arrays.sort() on the people array, it will be sorted by the last name:
Doe Doe Smith
In addition to sorting arrays of primitives, such as integers and doubles, Arrays.sort() can also be used to sort an array of objects. However, the objects must implement the Comparable interface in order to be sorted. This interface defines the compareTo() method, which specifies how objects should be compared to each other. For example:
class Person implements Comparable<Person> {
String name;
int age;
public Person(String name, int age) {
this.name = name;
this.age = age;
}
@Override
public int compareTo(Person other) {
return this.age - other.age;
}
}
Person[] people = {new Person("Alice", 30), new Person("Bob", 25), new Person("Charlie", 35)};
Arrays.sort(people);
The resulting sorted array will be sorted by age in ascending order, with the oldest person at the end.
It’s worth noting that Arrays.sort() has a time complexity of O(n log n) and a space complexity of O(1), making it an efficient choice for sorting arrays. This means that it can handle large arrays without causing performance issues.
It’s important to note that the Arrays.sort() method only works for arrays of primitives, such as integers and doubles, or objects that implement the Comparable interface. It cannot be used to sort arrays of objects that do not implement this interface. In those cases, you can use a Comparator or a custom sorting algorithm to sort the array.
Sorting an Array with a Comparator in Java
In addition to the built-in Arrays.sort() method, Java provides the option to sort an array of objects using a Comparator. A Comparator is an interface that defines how two objects should be compared. By implementing a Comparator, you can specify a custom sort order for your objects without modifying the objects themselves.
To use a Comparator to sort an array in Java, you need to follow these steps:
1. Create a class that implements the Comparator interface and overrides the compare() method. The compare() method takes two objects as arguments and returns an integer indicating their relative order. A positive value indicates that the first object should come after the second object, a negative value indicates that the first object should come before the second object, and a zero indicates that the objects are equal. Here is an example of a Comparator class that compares Person objects by last name:
class LastNameComparator implements Comparator<Person> {
public int compare(Person p1, Person p2) {
return p1.lastName.compareTo(p2.lastName);
}
}
2. Create an instance of your Comparator class. You can do this by calling the constructor of your Comparator class and storing the resulting object in a variable:
Comparator<Person> comparator = new LastNameComparator();
3. Call the Arrays.sort() method on the array you want to sort, passing the Comparator object as an argument. The Arrays.sort() method has the following syntax:
Arrays.sort(array, comparator);
Here is an example of using a Comparator to sort an array of Person objects:
Person[] people = {new Person("John", "Doe"), new Person("Jane", "Doe")};
Arrays.sort(people, comparator);
This will sort the people array in the order specified by the Comparator.
The complete code of using a Comparator to sort an array of Person objects by their last name:
class Person {
String firstName;
String lastName;
public Person(String firstName, String lastName) {
this.firstName = firstName;
this.lastName = lastName;
}
}
class LastNameComparator implements Comparator<Person> {
public int compare(Person p1, Person p2) {
return p1.lastName.compareTo(p2.lastName);
}
}
Person[] people = {new Person("John", "Doe"), new Person("Jane", "Doe")};
Arrays.sort(people, new LastNameComparator());
In this example, the LastNameComparator class implements the Comparator interface and overrides the compare() method to compare the last names of two Person objects. The Arrays.sort() method is then called on the people array, passing an instance of the LastNameComparator as an argument. This causes the array to be sorted by last name using the custom sort order specified in the Comparator.
Using a Comparator has several benefits. It allows you to specify a custom sort order without modifying the objects being sorted. This can be useful if you want to sort objects in a way that is different from their natural order, or if the objects do not implement the Comparable interface. It also allows you to sort objects of different types, as long as they can be compared using the Comparator.
On the other hand, using a Comparator requires you to write additional code to implement the Comparator interface. This can be more time-consuming than using the Comparable interface, which is implemented directly in the objects being sorted. However, the added flexibility of a Comparator can make it worth the extra effort in certain situations.
Sorting an Array with a Custom Algorithm
Custom algorithms offer a flexible way to sort arrays in Java. Instead of relying on built-in methods or comparators, you can implement your own sorting logic to fit the specific needs of your task.
There are several popular algorithms to choose from, including selection sort, insertion sort, bubble sort, merge sort, and quick sort. Each has its own set of pros and cons, and the appropriate choice depends on the specific requirements of your task. In this section, we will explore how to implement these algorithms to sort an array.
Selection Sort
Selection sort is a simple and intuitive algorithm that works by repeatedly selecting the smallest element from the unsorted portion of the array and placing it at the beginning.
To implement selection sort in Java, we can follow these steps:
- Iterate through the array with a loop, starting from the first element.
- At each iteration, find the minimum element in the unsorted portion of the array.
- Swap the minimum element with the current element.
- Repeat until the entire array is sorted.
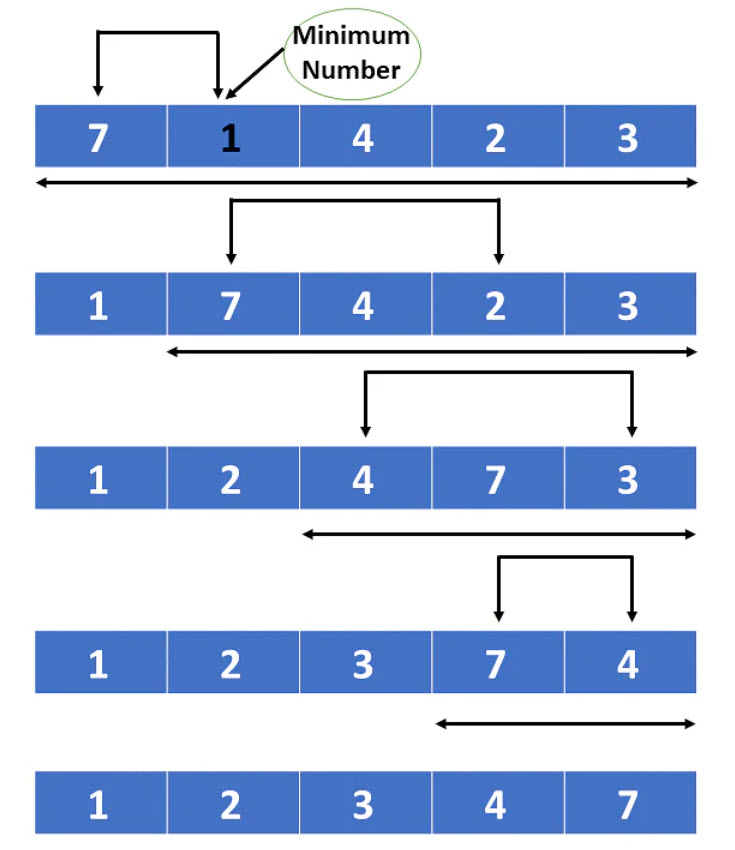
Selection Sort
Here is an example of selection sort implemented in Java:
public static void selectionSort(int[] array) {
for (int i = 0; i < array.length - 1; i++) {
int minIndex = i;
for (int j = i + 1; j < array.length; j++) {
if (array[j] < array[minIndex]) {
minIndex = j;
}
}
int temp = array[i];
array[i] = array[minIndex];
array[minIndex] = temp;
}
}
One advantage of selection sort is that it has a stable sort, meaning that the order of equal elements is preserved. However, it has a time complexity of O(n^2), which makes it less efficient for larger arrays.
Insertion Sort
Insertion sort is another simple and intuitive algorithm for sorting an array in Java. It works by iterating through the array and inserting each element into its proper place in the sorted portion of the array.
To implement insertion sort in Java, we can follow these steps:
- Start with the second element of the array.
- Compare the current element with the ones in the sorted portion of the array, moving from right to left.
- Insert the current element into its proper place by shifting the elements as necessary.
- Repeat until the entire array is sorted.
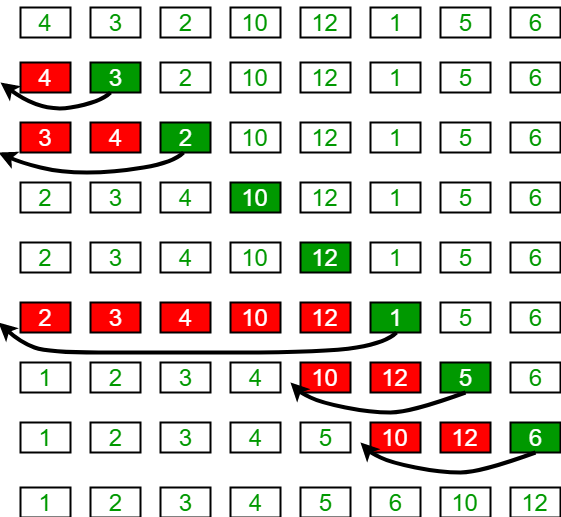
Insertion Sort
Here is an example of insertion sort implemented in Java:
public static void insertionSort(int[] array) {
for (int i = 1; i < array.length; i++) {
int current = array[i];
int j = i - 1;
while (j >= 0 && array[j] > current) {
array[j + 1] = array[j];
j--;
}
array[j + 1] = current;
}
}
Insertion sort is a stable sort, meaning that the order of equal elements is preserved. It has a time complexity of O(n^2) in the worst case, but it can be more efficient for smaller arrays or partially sorted arrays.
Bubble Sort
Bubble sort is a simple and easy-to-understand algorithm for sorting an array in Java. It works by repeatedly iterating through the array and swapping adjacent elements that are out of order.
To implement bubble sort in Java, we can follow these steps:
- Iterate through the array with a loop, starting from the first element.
- Compare each element with the one next to it. If the elements are out of order, swap them.
- Repeat the previous step until no more swaps are needed.
- Repeat the entire process until the array is sorted.
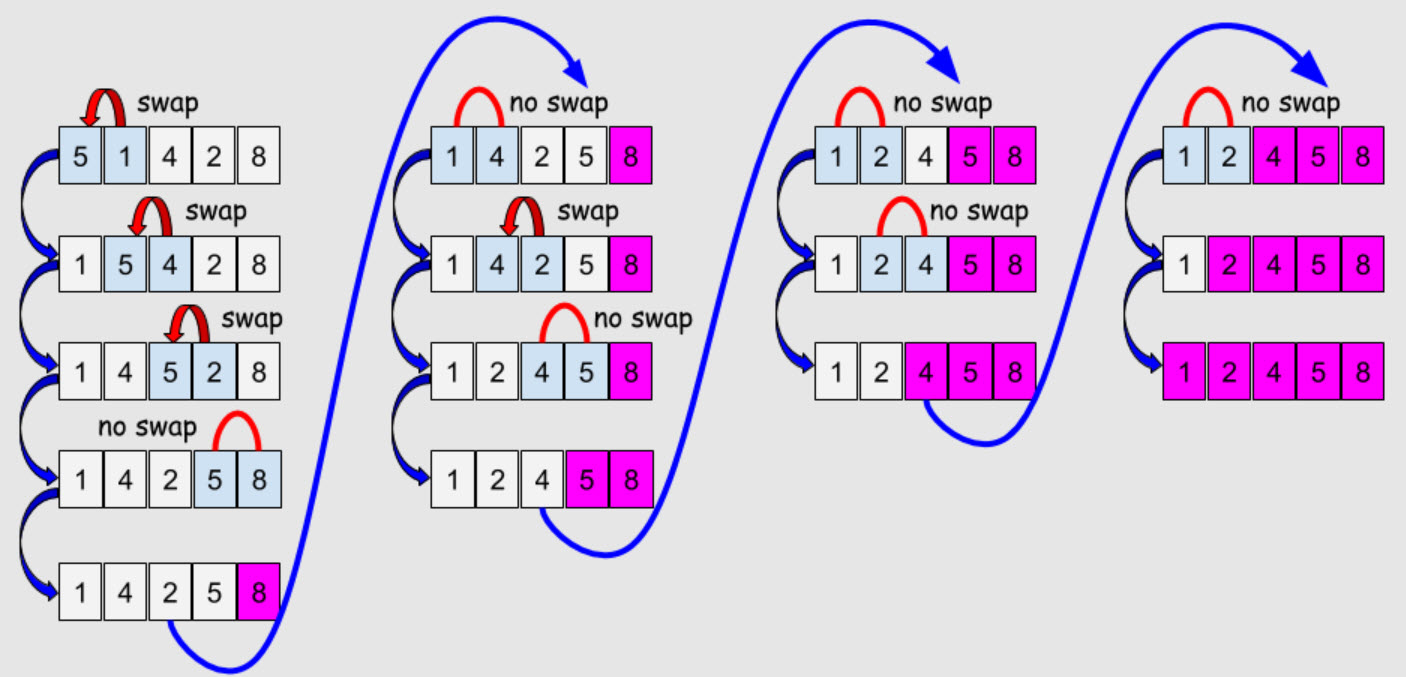
Bubble Sort
Here is an example of bubble sort implemented in Java:
public static void bubbleSort(int[] array) {
boolean sorted = false;
while (!sorted) {
sorted = true;
for (int i = 0; i < array.length - 1; i++) {
if (array[i] > array[i + 1]) {
int temp = array[i];
array[i] = array[i + 1];
array[i + 1] = temp;
sorted = false;
}
}
}
}
One advantage of bubble sort is that it is easy to understand and implement. However, it has a time complexity of O(n^2), which makes it less efficient for larger arrays. In addition, it is not a stable sort, meaning that the order of equal elements may not be preserved.
Merge Sort
Merge sort is a divide-and-conquer algorithm for sorting an array in Java. It works by repeatedly dividing the array into smaller subarrays, sorting the subarrays, and then merging them back together.
To implement merge sort in Java, we can follow these steps:
- Divide the array into two equal-sized subarrays.
- Recursively sort the left and right subarrays.
- Merge the sorted subarrays back together in a sorted manner.
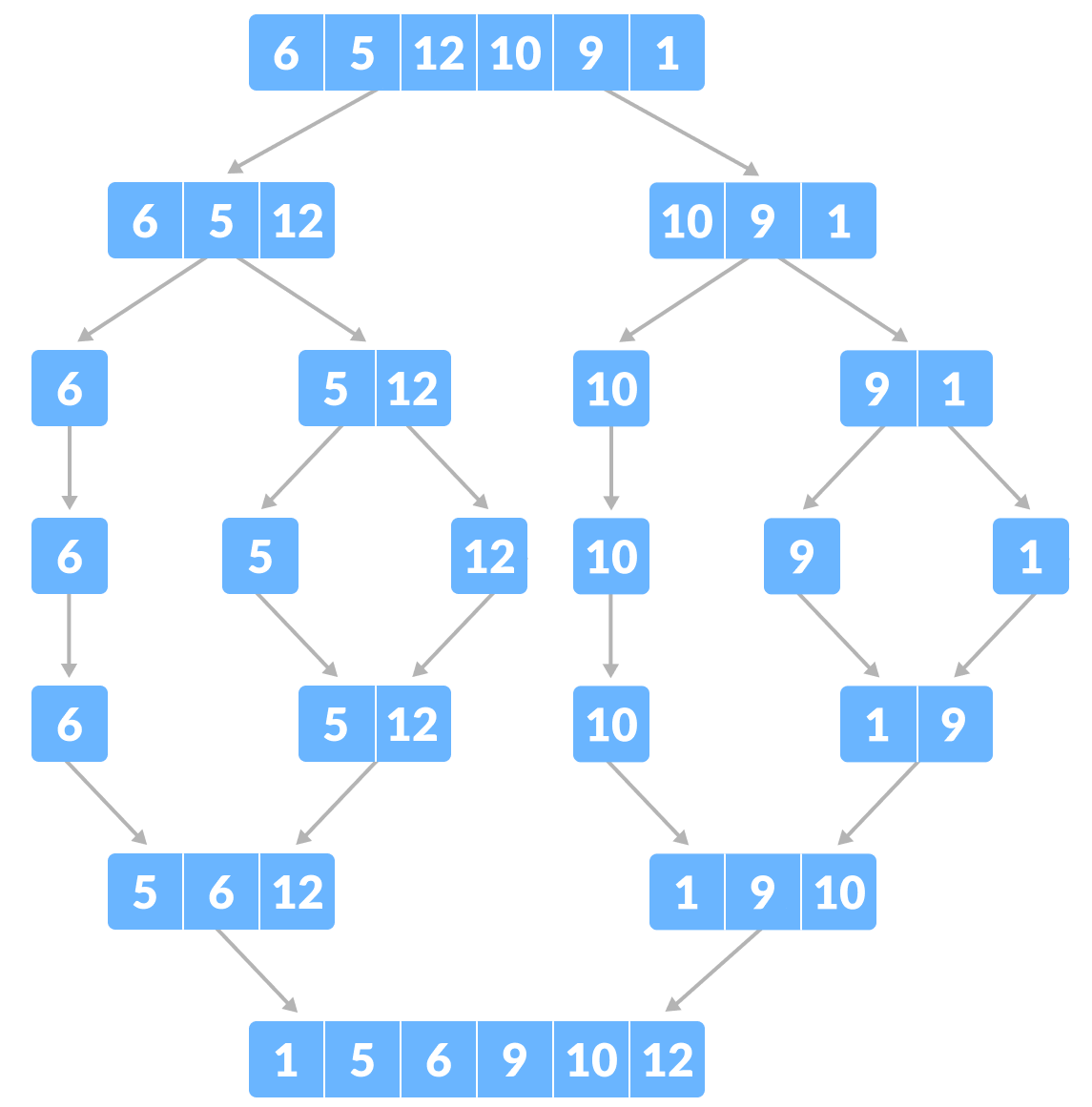
Merge Sort
Here is an example of merge sort implemented in Java:
public static void mergeSort(int[] array) {
if (array.length > 1) {
int mid = array.length / 2;
int[] left = Arrays.copyOfRange(array, 0, mid);
int[] right = Arrays.copyOfRange(array, mid, array.length);
mergeSort(left);
mergeSort(right);
merge(array, left, right);
}
}
public static void merge(int[] array, int[] left, int[] right) {
int i = 0, j = 0, k = 0;
while (i < left.length && j < right.length) {
if (left[i] < right[j]) {
array[k++] = left[i++];
} else {
array[k++] = right[j++];
}
}
while (i < left.length) {
array[k++] = left[i++];
}
while (j < right.length) {
array[k++] = right[j++];
}
}
Merge sort has a stable sort, meaning that the order of equal elements is preserved. It has a time complexity of O(n log n), which makes it more efficient for larger arrays. However, it has a space complexity of O(n) due to the auxiliary array required for merging.
Quick Sort
Quick sort is a popular and efficient algorithm for sorting an array in Java. It works by dividing the array into two subarrays, sorting them recursively, and then merging them back together.
To implement quick sort in Java, we can follow these steps:
- Choose a pivot element from the array.
- Divide the array into two subarrays, with all the elements less than the pivot in the first subarray and all the elements greater than the pivot in the second subarray.
- Sort the two subarrays recursively using the quick sort algorithm.
- Merge the sorted subarrays and the pivot element back together to form the final sorted array.
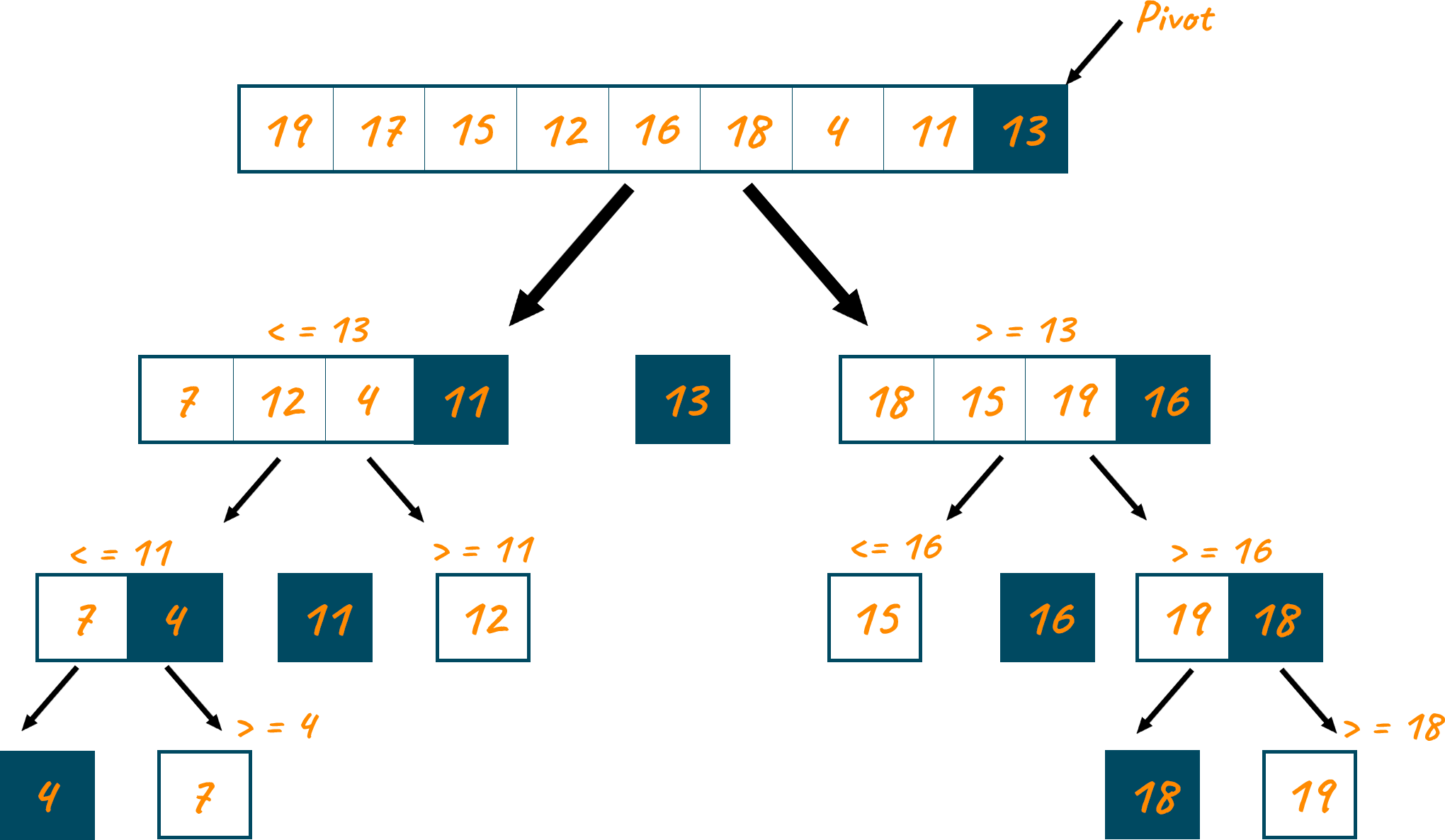
Quick Sort
Here is an example of quick sort implemented in Java:
public static void quickSort(int[] array, int left, int right) {
if (left < right) {
int pivotIndex = partition(array, left, right);
quickSort(array, left, pivotIndex - 1);
quickSort(array, pivotIndex + 1, right);
}
}
private static int partition(int[] array, int left, int right) {
int pivot = array[right];
int i = left - 1;
for (int j = left; j < right; j++) {
if (array[j] < pivot) {
i++;
int temp = array[i];
array[i] = array[j];
array[j] = temp;
}
}
int temp = array[i + 1];
array[i + 1] = array[right];
array[right] = temp;
return i + 1;
}
Quick sort has a time complexity of O(n log n) in the average case and O(n^2) in the worst case. It is not a stable sort, meaning that the order of equal elements may not be preserved.
Comparison the Methods of Sorting an Array in Java
When comparing the various methods of sorting an array in Java, there are several parameters that can be considered:
- Time complexity: The time complexity of a sorting algorithm determines how long it takes to sort an array of a given size. Some algorithms, like
Arrays.sort()and merge sort, have a time complexity of O(n log n), which makes them more efficient for larger arrays. Other algorithms, like selection sort, insertion sort, and bubble sort, have a time complexity of O(n^2), which makes them less efficient for larger arrays. Quick sort has a time complexity of O(n log n) in the average case, but it can degrade to O(n^2) in the worst case. - Space complexity: The space complexity of a sorting algorithm determines how much memory it requires to sort an array. Some algorithms, like
Arrays.sort()and insertion sort, have a space complexity of O(1), which means they do not require additional memory to sort the array. Other algorithms, like merge sort and quick sort, have a space complexity of O(n), which means they require additional memory proportional to the size of the array. - Stability: A stable sort is a sorting algorithm that preserves the order of equal elements. This can be important in some situations where the original order of the elements needs to be maintained.
Arrays.sort(), selection sort, insertion sort, and bubble sort are all stable sorts. Merge sort and quick sort are not stable sorts. - Ease of use: Some sorting algorithms are easier to understand and implement than others. For example,
Arrays.sort()is a built-in method that can be used with a single line of code, making it very easy to use. Selection sort, insertion sort, and bubble sort are also relatively simple algorithms that are easy to understand and implement. Merge sort and quick sort are more complex algorithms that may require more effort to understand and implement. - Performance: The performance of a sorting algorithm can vary depending on the specific characteristics of the array being sorted. Some algorithms may perform better on certain types of arrays than others. It is important to benchmark and test the performance of different algorithms in order to choose the most appropriate one for a given task.
Here is a comparison table for the different methods of sorting arrays in Java:
| Method | Time complexity | Space complexity | Stability | Ease of use | Performance |
|---|---|---|---|---|---|
| Arrays.sort() | O(n log n) | O(1) | Yes | High | Good |
| Comparator | O(n log n) | O(1) | Yes | High | Good |
| Selection sort | O(n^2) | O(1) | Yes | High | Poor |
| Insertion sort | O(n^2) | O(1) | Yes | High | Fair |
| Bubble sort | O(n^2) | O(1) | Yes | High | Poor |
| Merge sort | O(n log n) | O(n) | Yes | Low | Good |
| Quick sort | O(n log n) | O(log n) | No | Low | Good |
All of the methods for sorting arrays in Java have their own strengths and weaknesses. Arrays.sort() and the Comparator interface are easy to use and have good performance, but they may not be suitable for large arrays or for custom sorting needs. Selection sort, insertion sort, and bubble sort are simple and easy to understand, but they have poor performance for larger arrays. Merge sort is efficient and stable, but it requires additional space. Quick sort is also efficient, but it is not stable and may not be suitable for certain applications.
When sorting an array in Java, the best method to use depends on the specific requirements of the task. Here are some general guidelines:
- If stability and ease of use are important, then
Arrays.sort(),Comparator, or one of the stable sorts (selection sort, insertion sort, bubble sort, or merge sort) may be the best choice. - If performance is the main concern and the array is relatively large, then quick sort may be the best choice.
- For smaller arrays,
Arrays.sort()or merge sort may be the most efficient options.
It is important to consider all of the relevant parameters, such as time complexity, space complexity, stability, ease of use, and performance, when deciding which method to use.
Conclusion
In this article, we discussed several options for sorting an array in Java.
One option is to use the built-in Arrays.sort() method, which has a time complexity of O(n log n) and a space complexity of O(1). It is easy to use and works well for most cases, but it requires the objects in the array to implement the Comparable interface.
Another option is to use a Comparator, which allows you to specify a custom comparison function for sorting the array. This is useful when the objects in the array do not implement the Comparable interface or when you want to sort the array in a specific way that is not provided by the default compareTo() method.
Finally, we discussed several custom sorting algorithms that can be implemented in Java, including selection sort, insertion sort, bubble sort, merge sort, and quick sort. These algorithms have different time and space complexities, and they may be more or less suitable depending on the specific requirements of the task.

