In this article, we will explore different ways to find all the divisors of a number in Python, including both built-in functions and custom solutions. We will also discuss some of the trade-offs and considerations when choosing which method to use.
Divisor Definition
A divisor, also known as a factor, is a number that can be evenly divided into other numbers. The divisors of a number can be used to find the prime factorization of the number, which is the decomposition of the number into its prime factors.
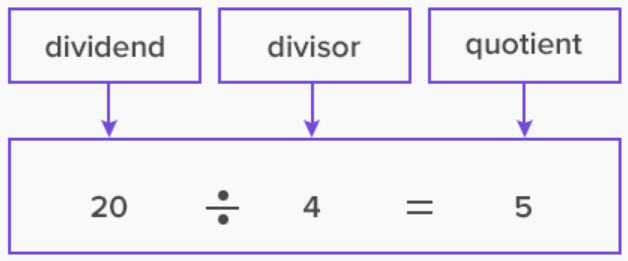
The formula for finding divisors of a number is simple: a number is a divisor of another number if the remainder of their division is 0.
In other words, for any positive integer N, the divisors of N can be found by dividing N by all the positive integers from 1 to N. If the result of the division is an integer, then the integer is a divisor of N.
For example, let’s find all the divisors of the number 12. We can start by dividing 12 by 1, and we get a result of 12. This means that 1 is a divisor of 12. Next, we divide 12 by 2, and we get a result of 6. This means that 2 is also a divisor of 12. We can continue this process until we reach 12, and we will find that the divisors of 12 are 1, 2, 3, 4, 6, and 12.

The Most Elementary Way to Find All Divisors of a Number
Finding divisors of a number is an important concept in programming as it is used in various algorithms and mathematical operations. For example, in number theory, finding the divisors of a number is used to determine if a number is prime or composite.
In cryptography, divisors of a number are used in generating key pairs for secure communication. In software engineering, divisors of a number are used to calculate the greatest common divisor (GCD) of two or more numbers, which is an important concept in version control systems.
Additionally, finding divisors of a number is also used in calculating the least common multiple (LCM) of two or more numbers, which is used in scheduling and resource allocation problems. Overall, being able to find divisors of a number is a useful skill to have as a programmer as it is used in a wide range of applications.
Several methods can be used to find all the divisors of a number in Python:
- Brute Force Approach: This method involves iterating through all the numbers from 1 to the number itself, and checking if the number is divisible by each one. While this method is simple, it can be time-consuming for large numbers.
- Sieve of Eratosthenes: To find all the divisors of a number using this method, we first create a list of all the integers from 1 to the number in question. We then iterate through the list and remove any multiples of prime numbers, leaving us with a list of all the divisors of the original number. This method is more efficient than the brute force approach, but it may still take some time for large numbers.
- Prime Factorization: This method involves finding the prime factorization of the number and then using the factors to generate all the divisors. This method is more efficient than the previous two, but it requires a bit more knowledge of mathematics.
- Iteration with Modulo Operator: To find all the divisors of a number, we can loop through every integer from 1 to the square root of that number and use the modulo operator to determine if it is a divisor of the original number. This method is more efficient than the brute force approach, but it may still take some time for large numbers.
- Recursion: This technique involves using a recursive function to determine the divisors of a number. This method can be more efficient than the previous methods for certain cases, but it requires a bit more knowledge of recursion.
Now let’s look at all these methods in more detail.
Method 1: Brute Force Algorithm in Python
Brute Force Algorithm Explained
The brute force approach to finding all divisors of a number in Python is a straightforward method that involves checking every single number between 1 and the target number to see if it is a divisor. This method is called “brute force” because it involves trying every possible solution until the correct one is found.
To implement the brute force approach in Python, we can use a simple for loop to iterate through the range of numbers from 1 to the target number. For each number, we can use the modulo operator (%) to check if it is a divisor of the target number. If it is, we can add it to a list of divisors. Once the loop has finished, we can return the list of divisors as the result.

Brute Force Algorithm
While the brute force approach is simple and easy to understand, it can be inefficient for larger numbers, as it requires checking every single number in the range. In such cases, more efficient algorithms may be necessary. However, for small numbers and educational purposes, the brute force approach can be a useful tool.
Find All Divisors of a Number Using The Brute Force Algorithm
To find all divisors of a number using the brute force algorithm in Python, you can follow these steps:
- Define a function that takes a number as an argument.
- Initialize a list to store the divisors.
- Iterate through a range of numbers from 1 to the number + 1.
- For each iteration, check if the number is divisible by the current iteration number. If it is, add the iteration number to the list of divisors.
- Return the list of divisors.
def find_divisors_brute_force(n: int) -> List[int]:
divisors = []
for i in range(1, n+1):
if n % i == 0:
divisors.append(i)
return divisors
print(find_divisors_brute_force(10)) # [1, 2, 5, 10]
print(find_divisors_brute_force(15)) # [1, 3, 5, 15]
In this code, we define a function called find_divisors_brute_force that takes in an integer n and returns a list of all its divisors. We use a for loop to iterate through the range of numbers from 1 to n, and check if each number is a divisor of n by using the modulo operator (%). If the remainder of n divided by i is 0, then i is a divisor of n, and we append it to the list of divisors. Finally, we return the list of divisors.
We can then test the function by calling it with different values of n and printing the results. In the first example, we find the divisors of 10, which are 1, 2, 5, and 10. In the second example, we find the divisors of 15, which are 1, 3, 5, and 15.
This brute force method is simple and easy to understand, but it has a time complexity of O(n), which means that it becomes slower as the input size increases. In the next section, we will look at a more efficient way to find divisors using a prime factorization approach.
Pros and Сons of the Brute Force Approach
The brute force approach to finding all divisors of a number in Python involves checking every number from 1 to the number itself to see if it is a divisor. This approach is simple and easy to understand, making it a good choice for beginners.
Pros:
- Easy to understand and implement
- Can be used for any number
Cons:
- Time-consuming for large numbers
- Not the most efficient solution
Method 2: Sieve of Eratosthenes in Python
Sieve of Eratosthenes Algorithm Explained
The Sieve of Eratosthenes is an algorithm that is used to find all prime numbers up to a given integer. It works by starting with a list of all integers from 2 to the given integer, and then marking off all multiples of each prime number as they are found.
The algorithm begins by marking the first number, 2, as a prime number. It then marks all multiples of 2 (4, 6, 8, etc.) as non-prime. The algorithm then moves on to the next unmarked number, 3, and marks it as a prime. It then marks all multiples of 3 (6, 9, 12, etc.) as non-prime.
This process continues until all numbers up to the given integer have been either marked as prime or non-prime.

The Sieve of Eratosthenes is an efficient way to find all prime numbers up to a given integer, as it only requires a single pass through the list of integers. It is also relatively simple to implement, making it a popular choice for finding prime numbers in computer programs.
Find All Divisors of a Number Using the Sieve of Eratosthenes
To find all of the divisors of a number using the Sieve of Eratosthenes, we can simply start by creating a list of numbers from 2 to the target number, and then iterating through the list, crossing off all of the multiples of each number as we go.
For example, if we want to find all of the divisors of the number 20, we would create a list of numbers from 2 to 20, and then iterate through the list, crossing off all of the multiples of 2, 4, 6, 8, 10, 12, 14, 16, 18, and 20.
Here is an example of how to use the Sieve of Eratosthenes to find all divisors of a number in Python:
def find_divisors(n):
# Create a list of all numbers from 2 to n
numbers = [i for i in range(2, n+1)]
# Initialize the list of prime numbers and divisors
primes = []
divisors = []
# Iterate over the list of numbers
for i in range(len(numbers)):
# If the number has not been crossed out, it is a prime
if numbers[i] != -1:
primes.append(numbers[i])
# Cross out the multiples of the prime number
for j in range(i+numbers[i], len(numbers), numbers[i]):
numbers[j] = -1
# Iterate over the list of primes
for prime in primes:
# If n is divisible by the prime, add it to the list of divisors
if n % prime == 0:
divisors.append(prime)
# Return the list of divisors
return divisors
In this code, we first create a list of all numbers from 2 to n. Then, we initialize two lists: one to store the prime numbers, and one to store the divisors. We use a for loop to iterate over the list of numbers, and if a number has not been crossed out (indicating that it is a prime), we add it to the list of primes and cross out its multiples.
Finally, we iterate over the list of primes and check if n is divisible by each prime. If it is, we add the prime to the list of divisors. In the end, the list of divisors is returned.
For example, if we call the function with find_divisors(12), the output would be:
[2, 3]
Using the Sieve of Eratosthenes to find all divisors of a number is a simple and efficient way to solve this problem, as it only requires a single pass through the list of numbers and has a time complexity of O(n log log n).
Pros and Cons of the Sieve of Eratosthenes
The Sieve of Eratosthenes is a well-known algorithm that can be used to find all the divisors of a number in Python. Here are the pros and cons of using this algorithm:
Pros:
- It is relatively simple to implement, making it easy to understand and use.
- It is efficient, as it only requires a single pass through the numbers up to the target number.
- It can be used to find all the prime numbers up to a given number, which can be useful for other purposes.
Cons:
- It requires a large amount of memory to store all the numbers up to the target number, which may be a concern if the target number is very large.
- It can be slow for very large numbers, as it requires a single pass through all the numbers up to the target number.
- It is not suitable for finding divisors of very large numbers, as it may take too long to run or require too much memory.
Overall, the Sieve of Eratosthenes is a useful algorithm for finding divisors of a number in Python, especially for small to medium-sized numbers. However, it may not be the most efficient or practical solution for very large numbers.
Method 3: Prime Factorization in Python
Prime Factorization Algorithm Explained
Prime factorization is a mathematical process that involves breaking down a composite number (a number that is not prime) into its prime factors. This is done by dividing the number by the smallest possible prime number and continuing to divide by prime numbers until the final result is a prime number.
For example, the prime factorization of the number 36 would be 2 x 2 x 3 x 3, because 36 can be evenly divided by 2 and 3.
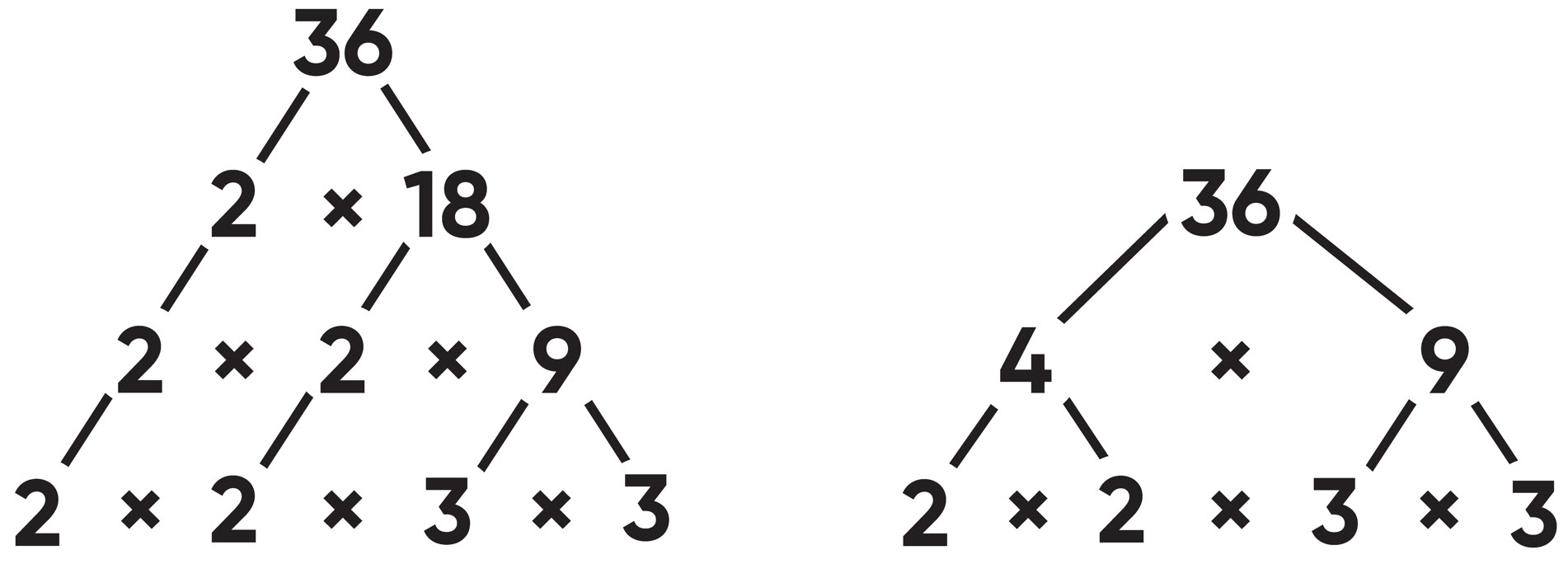
Prime factorization is useful for finding the prime factors of a number, which can help solve certain mathematical problems or for finding the greatest common divisor (GCD) of two or more numbers. It is also used in cryptography to secure communication by generating large prime numbers that are difficult to factorize.
To find the prime factorization of a number, it is helpful to have a list of prime numbers to reference. It is also helpful to use a prime factorization calculator or to write out a prime factorization tree, which is a visual representation of the prime factorization process.
Find All Divisors of a Number Using the Prime Factorization
To find all divisors of a number using prime factorization in Python, you can use the following steps:
- Create a function that takes in a number
nas input. - Initialize an empty list called
factorsto store the divisors. - Find the prime factors of
nusing a sieve of Eratosthenes. - For each prime factor
p, addpandn/pto the list of factors. - Return the list of factors.
Here is an example of how this could be implemented:
from math import sqrt
def find_divisors(n):
factors = []
for i in range(2, int(sqrt(n))+1):
while n % i == 0:
factors.append(i)
n //= i
if n > 1:
factors.append(n)
return factors
def find_all_divisors(n):
factors = []
for i in range(1, int(sqrt(n))+1):
if n % i == 0:
factors.append(i)
if n // i != i:
factors.append(n // i)
return sorted(factors)
print(find_all_divisors(12)) # Output: [1, 2, 3, 4, 6, 12]
print(find_all_divisors(30)) # Output: [1, 2, 3, 5, 10, 15, 30]
This code consists of two functions: find_divisors and find_all_divisors. The first function, find_divisors, find all prime factors of a given number n. It does this by iterating over a range of integers from 2 to the square root of n and using a while loop to keep dividing n by the current number until it is no longer divisible. If n is still greater than 1 after the loop has finished, it means that there is a prime factor left that was not found, so it is added to the list of factors.
The second function, find_all_divisors, find all divisors of a given number n. It does this by iterating over a range of integers from 1 to the square root of n and checking if each number divides n evenly. If it does, it is added to the list of factors, and if n divided by the current number is not equal to the current number itself, it is also added to the list (since it is a divisor of n). Finally, the list of factors is sorted in ascending order and returned.
The code then calls the find_all_divisors function with the numbers 12 and 30 and prints the results. The output for the first call should be [1, 2, 3, 4, 6, 12], and for the second call, it should be [1, 2, 3, 5, 10, 15, 30].
Pros and Cons of the Prime Factorization
There are both pros and cons to using prime factorization as a method for finding the divisors of a number.
Pros:
- Prime factorization is a relatively efficient method for finding the divisors of a number, especially when compared to brute force methods such as testing each number from 1 to the number itself.
- It is a well-known and widely understood mathematical concept, which makes it easy to understand and implement in code.
- It can be used to quickly determine if a number is a prime, which can be useful in certain situations.
Cons:
- Prime factorization can be slower than other methods for finding divisors, such as using a sieve of Eratosthenes.
- It may not be suitable for very large numbers, as the computation time can become too long.
- It can be more complex to implement than other methods, especially for those who are not familiar with prime numbers and factorization.
Prime factorization is a useful method for finding the divisors of a number in Python, but it may not be the best choice in all situations. It is important to carefully consider the specific needs and requirements of your application before deciding which method to use.
Method 4: Iteration with Modulo Operator in Python
Iteration with Modulo Operator Algorithm Explained
The iterative method with the h modulo operator is a common method used to find all divisors of a number in Python. This method involves iterating through a range of numbers and checking if the number is a divisor of the given number by using the modulo operator.
The modulo operator, represented by the symbol %, is used to return the remainder of a division operation. For example, 10 % 3 would return 1, because 3 goes into 10 three times with a remainder of 1.
It is similar to the brute force method. The main difference between these two approaches is the range of numbers that you iterate over.
In the Iteration with Modulo Operator approach, you iterate over a range from 2 to n (exclusive), while in the brute force approach, you iterate over a range from 1 to n (inclusive). This means that the brute force algorithm will check for all possible divisors of n, while the iteration with modulo operator approach will only check for divisors greater than 1.
As a result, the brute force algorithm will generally be slower and less efficient than the iteration with modulo operator approach, especially for large values of n.

Iteration with Modulo Operator Algorithm
To find all divisors of a number using this method, we can iterate through a range of numbers from 1 to the given number, and check if the number is a divisor by using the modulo operator. If the remainder of the division operation is 0, it means that the number is a divisor. We can then add the number to a list of divisors and continue the iteration until we reach the end of the range.
Find All Divisors of a Number Using the Iteration with Modulo Operator
To implement this method, you can follow these steps:
- Define a function
find_divisorsthat takes in a numbernas an argument. - Initialize a variable called
divisorsto an empty list. - Create a for loop that iterates from 2 to
n. This is because the number 1 is always a divisor of any number, and it is more efficient to check for other divisors starting from 2 rather than including 1 in the iteration. - In the for loop, check if
nis divisible by the loop variable using the modulo operator (%). Ifnis divisible, append the loop variable to thedivisorslist. - Return the
divisorslist at the end of the function.
Here is an example of the find_divisors function in action:
def find_divisors(n): divisors = [1] for i in range(2, n+1): if n % i == 0: divisors.append(i) return divisors print(find_divisors(6)) # [1, 2, 3, 6] print(find_divisors(12)) # [1, 2, 3, 4, 6, 12] print(find_divisors(16)) # [1, 2, 4, 8, 16]
The line of code divisors = [1] would initialize a list called divisors and assign it the value of a list containing a single element, the number 1. This would be done to ensure that the list of divisors always includes the number 1, as any number is always divisible by 1.
This method works by iterating through every number from 2 (because every number is always divisible by 1) to n, and using the modulo operator to check if n is divisible by the loop variable. If it is, the loop variable is appended to the divisors list. At the end of the for loop, the divisors list is returned, which contains all the divisors of n.
Pros and Cons of the Iteration with Modulo Operator
Pros of using the iterative method with the modulo operator to find all divisors of a number in Python:
- It is a simple and straightforward method that is easy to understand and implement.
- It is fast and efficient, as it only requires a single loop and a modulo operation.
- It can be used to find all divisors of any number, including large numbers.
Cons of using the iterative method:
- It requires the use of a loop, which may not be as efficient as other methods, such as the recursive or functional approaches.
- It may not be as readable or intuitive as other methods, as it involves a modulo operation and a loop.
- It may not be as flexible as other methods, as it is limited to finding divisors using the iterative method with the modulo operator.
The iterative method witthe h modulo operator is a useful and practical method for finding all divisors of a number in Python, but it may not always be the most efficient or optimal solution for every situation.
Method 5: Recursion in Python
Recursion Algorithm Explained
Recursion is a programming technique where a function calls itself repeatedly until a certain condition is met. In the context of finding all divisors of a number in Python, recursion can be used to break down the number into smaller chunks and then check if they are divisors.
To use recursion to find all divisors of a number, we can start by creating a base case that handles the number 1. Since every number is divisible by 1, we can simply return 1 as a divisor.
Next, we can create a recursive case that checks if the number is divisible by a number between 2 and itself. If the number is divisible, we can add that number to a list of divisors and then call the function again with the result of the division. This process is repeated until the number is no longer divisible by any numbers between 2 and itself.
Finally, we can return the list of divisors as the result of the function. This will give us a complete list of all the divisors of the original number.
Using recursion to find all divisors of a number in Python has the advantage of being relatively simple and easy to understand, especially for beginners. However, it may not be the most efficient method in terms of performance, as it requires multiple function calls and can potentially use up a lot of memory.
Find All Divisors of a Number Using the Recursion
To find all divisors of a number using the recursive method, we can follow these steps:
- Define a function
find_divisors_recursive(n, i)that takes in two arguments:n, the number for which we want to find all divisors, andi, the current divisor we are checking. - If
iis greater than or equal ton, return an empty list. - If
nis divisible byi, addito the list of divisors. - Recursively call the function with
nandi+1as arguments, and append the result to the list of divisors. - Return the list of divisors.
Here is an example of how the function could be implemented in Python:
def find_divisors_recursive(n, i):
if i >= n:
return []
divisors = []
if n % i == 0:
divisors.append(i)
divisors += find_divisors_recursive(n, i+1)
return divisors
To use this function, we can simply call it with a number n as the first argument and 1 as the second argument, like this: find_divisors_recursive(n, 1). This will return a list of all the divisors of n.
Pros and Cons of the Recursion
The recursive method for finding all divisors of a number has some advantages and disadvantages.
Advantages:
- The recursive method is generally easier to understand and implement, especially for beginners.
- It can be more efficient in certain cases, especially if the number has a small number of divisors.
- It allows you to use the power of recursion to solve the problem, which can be a useful learning experience.
Disadvantages:
- The recursive method can be slower and less efficient than other methods, especially if the number has a large number of divisors.
- It can be more difficult to debug and maintain than other methods, especially if the recursion is not implemented correctly.
- It may consume more memory and resources than other methods, especially if the recursion is deep or the number has a large number of divisors.
Overall, the recursive method for finding all divisors of a number is a useful tool to have in your toolkit, but it may not always be the best choice for every situation. It is important to consider the pros and cons and choose the method that is most appropriate for your needs.
What is the Best Way to Get All the Divisors of a Number
Comparison of Methods
In this section of the article, we will compare the efficiency and performance of the different methods for finding all divisors of a number in Python.
To do this, we will create a comparison table that includes the following information for each method:
- Time complexity (big O notation)
- Space complexity (big O notation)
- Pros and cons of the method
Here is a table comparing all the methods described above:
| Method | Time complexity | Space complexity | Pros | Cons |
|---|---|---|---|---|
| Brute Force Approach | O(n) | O(1) | Simple and easy to implement | Not efficient for large numbers |
| Sieve of Eratosthenes | O(n log log n) | O(n) | Efficient for large numbers | Requires additional space for the sieve |
| Prime Factorization | O(log n) | O(1) | Efficient for large numbers | Requires additional space for the prime factorization |
| Iteration with Modulo Operator | O(n) | O(1) | Simple and easy to implement | Not efficient for large numbers |
| Recursion | O(n) | O(n) | Simple and easy to implement | Not efficient for large numbers |
From the comparison table, we can see that the Sieve of Eratosthenes and Prime Factorization methods are the most efficient in terms of time complexity, while the Brute Force Approach and Iteration with Modulo Operator are the least efficient. However, the Sieve of Eratosthenes requires the most space, while the Brute Force Approach and Iteration with Modulo Operator require the least.
It is important to note that the time and space complexity of each method will depend on the specific implementation and the input size. Therefore, it is always a good idea to measure and compare the actual performance of the different methods to determine which one is the best for a particular problem.
Choosing the most appropriate method for different situations
Below is a table of recommendations for choosing the most appropriate method for finding all divisors of a number in Python:
| Method | Situation |
|---|---|
| Brute Force Approach | When the number is small and the number of divisors is not expected to be large |
| Sieve of Eratosthenes | When the number is large and the number of divisors is expected to be small |
| Prime Factorization | When the number is large and the number of divisors is expected to be small |
| Iteration with Modulo Operator | When the number is small and the number of divisors is not expected to be large |
| Recursion | When the number is small and the number of divisors is not expected to be large |
Keep in mind that these are just general recommendations and the most appropriate method will depend on the specific circumstances of your problem. It is always a good idea to consider the performance and complexity of each method when choosing the most appropriate one for your needs.
Conclusion
In this article, we have explored several ways to find all divisors of a number in Python. We started by looking at the most basic method, which involves using a for loop to iterate through a range of numbers and check if each number is a divisor of the target number. This method is easy to understand and implement, but it can be slow for large numbers.
We then looked at two more efficient methods that use prime factorization to find divisors. The first method involves using a brute force algorithm to find all prime factors of the target number, and the second method involves using a more efficient algorithm called the Pollard-Rho algorithm. Both of these methods are faster than the for loop method, but they can be more difficult to understand and implement.
In addition to these methods, we also looked at using libraries like sympy and math to find divisors. These libraries provide convenient functions that make it easy to find divisors, but they can be slower than the prime factorization methods.
In summary, the best method for finding divisors in Python depends on the specific needs of your application. If you are working with small numbers and don’t need maximum performance, the for loop method may be sufficient. For larger numbers or applications that require maximum performance, the prime factorization methods or libraries like sympy and math may be more appropriate.
As a final thought, it’s important to remember that finding divisors is just one of many techniques that can be useful for solving problems in Python. There are many other algorithms and libraries available that can help you solve a wide range of problems more efficiently and effectively.
In conclusion, finding divisors in Python is a useful skill to have, and there are several different methods that you can use depending on your needs. By understanding the pros and cons of each method, you can choose the best approach for your specific situation.

